pacman::p_load(tidyverse, sf, tmap)In-class Exercise 3: Anaytical Mapping
1 Getting Started
Installing and loading packages
Importing data
Import NGP_wp.rds created in In-class Exercise 2
NGA_wp <- read_rds("data/rds/NGA_wp.rds")2 Basic Choropleth Mapping
2.1 Choropleth map of functional water points
p1 <- tm_shape(NGA_wp) +
tm_fill("wp_functional", n = 10,
style = "equal",
palette = "Blues")+
tm_borders(lwd = 0.1,
alpha=1) +
tm_layout(main.title = "Distribution of functional water points by LGA", legend.outside=FALSE)2.2 Choropleth of total water points
p2 <- tm_shape(NGA_wp) +
tm_fill("total_wp", n = 10,
style = "equal",
palette = "Blues")+
tm_borders(lwd = 0.1,
alpha=1) +
tm_layout(main.title = "Total water points by LGA", legend.outside=FALSE)tmap_arrange(p2, p1, nrow=1)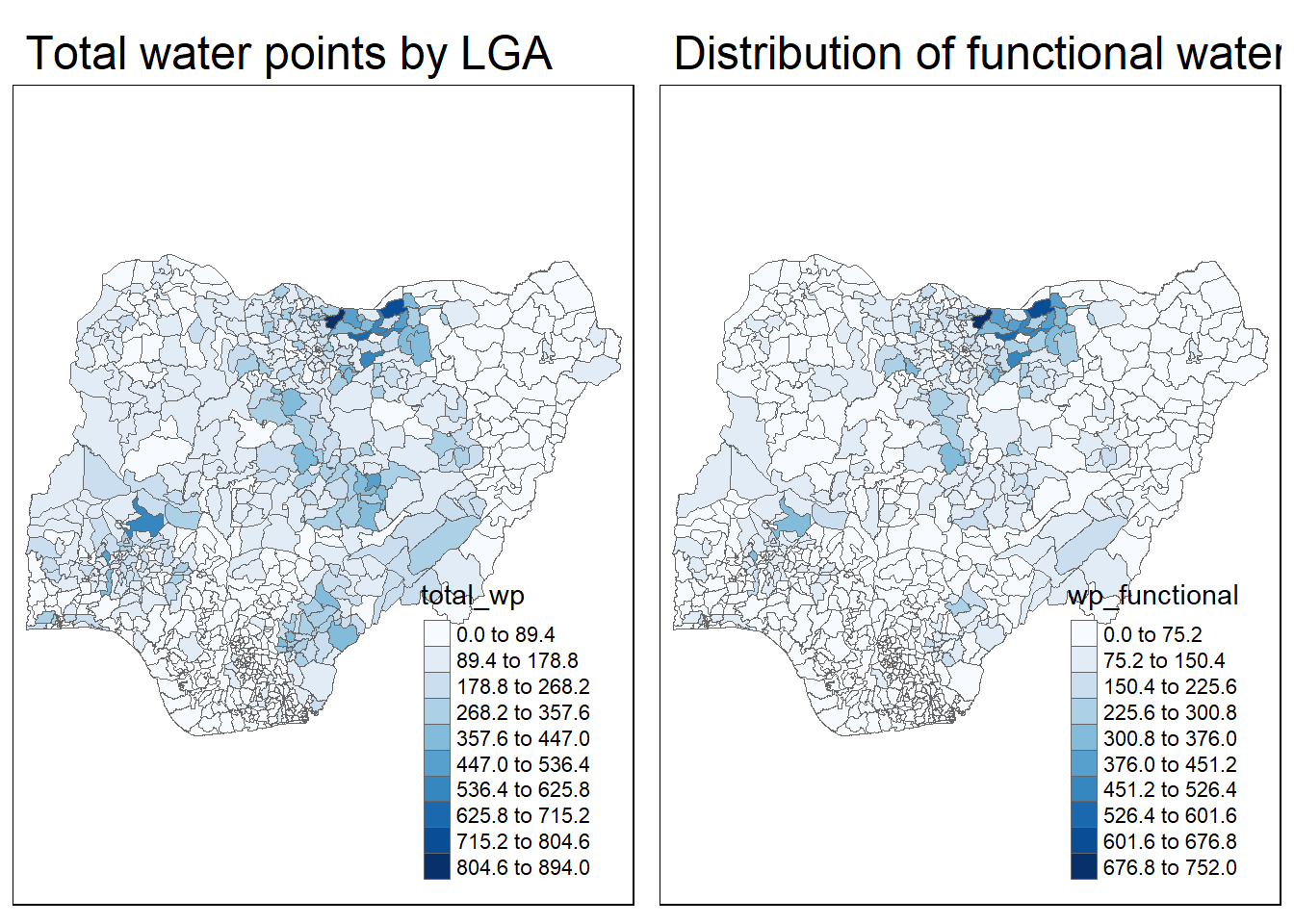
3 Choropleth Map - percentage
However, the above 2 maps display the total and functional water points by absolute value. By using the percentage function to view the percentage of functional to total number of water points, we see a dichotomous distribution of water points in Nigeria.
Calculating percentage of functional water points
NGA_wp <- NGA_wp %>%
mutate(pct_functional = wp_functional/total_wp) %>%
mutate(pct_nonfunctional = wp_nonfunctional/total_wp)3.1 Plotting
tm_shape(NGA_wp)+
tm_fill("pct_functional",
n=10,
style="equal",
palette="Blues",
legend.hist = TRUE) +
tm_borders(lwd=0.1,
alpha=1)+
tm_layout(main.title="Rate map of functional water points",
legend.outside = TRUE)
4 Extreme Values Mapping
Mapping extreme values to highlight the values at the upper and lower scale of the dataset and easily visualise outliers.
4.1 Percentile Map
4.1.1 Data preparation
Step 1: Removing NA values
NGA_wp <- NGA_wp %>% drop_na()Step 2: Customised classification and extracting values
percent <- c(0,.01,.1,.5,.9,.99,1)
var <- NGA_wp["pct_functional"] %>%
st_set_geometry(NULL)
quantile(var[,1], percent) 0% 1% 10% 50% 90% 99% 100%
0.0000000 0.0000000 0.2169811 0.4791667 0.8611111 1.0000000 1.0000000 4.1.2 Functions
Mapping functions that simplify the mapping process and reduces the likelihood of mistakes
4.1.3 get.var function
Extracts a variable (i.e. wp_nonfunctional) as a vector out of an sf data.frame.
inputs:
vname: variable name
df: name of the sf data frame
output:
- v: a vector with values
get.var <- function(vname,df){
v<- df[vname] %>%
st_set_geometry(NULL)
v<- unname(v[,1])
return(v)
}4.1.4 Percentile function
percentmap <- function(vnam, df, legtitle=NA, mtitle="Percentile Map"){
percent <- c(0,.01,.1,.5,.9,.99,1)
var <- get.var(vnam, df)
bperc <- quantile(var, percent)
tm_shape(df) +
tm_polygons() +
tm_shape(df) +
tm_fill(vnam,
title=legtitle,
breaks=bperc,
palette="Blues",
labels=c("< 1%", "1% - 10%", "10% - 50%", "50% - 90%", "90% - 99%", "> 99%")) +
tm_borders() +
tm_layout(main.title = mtitle,
title.position = c("right","bottom"))
}4.1.5 Running or Calling the function
percentmap("total_wp", NGA_wp)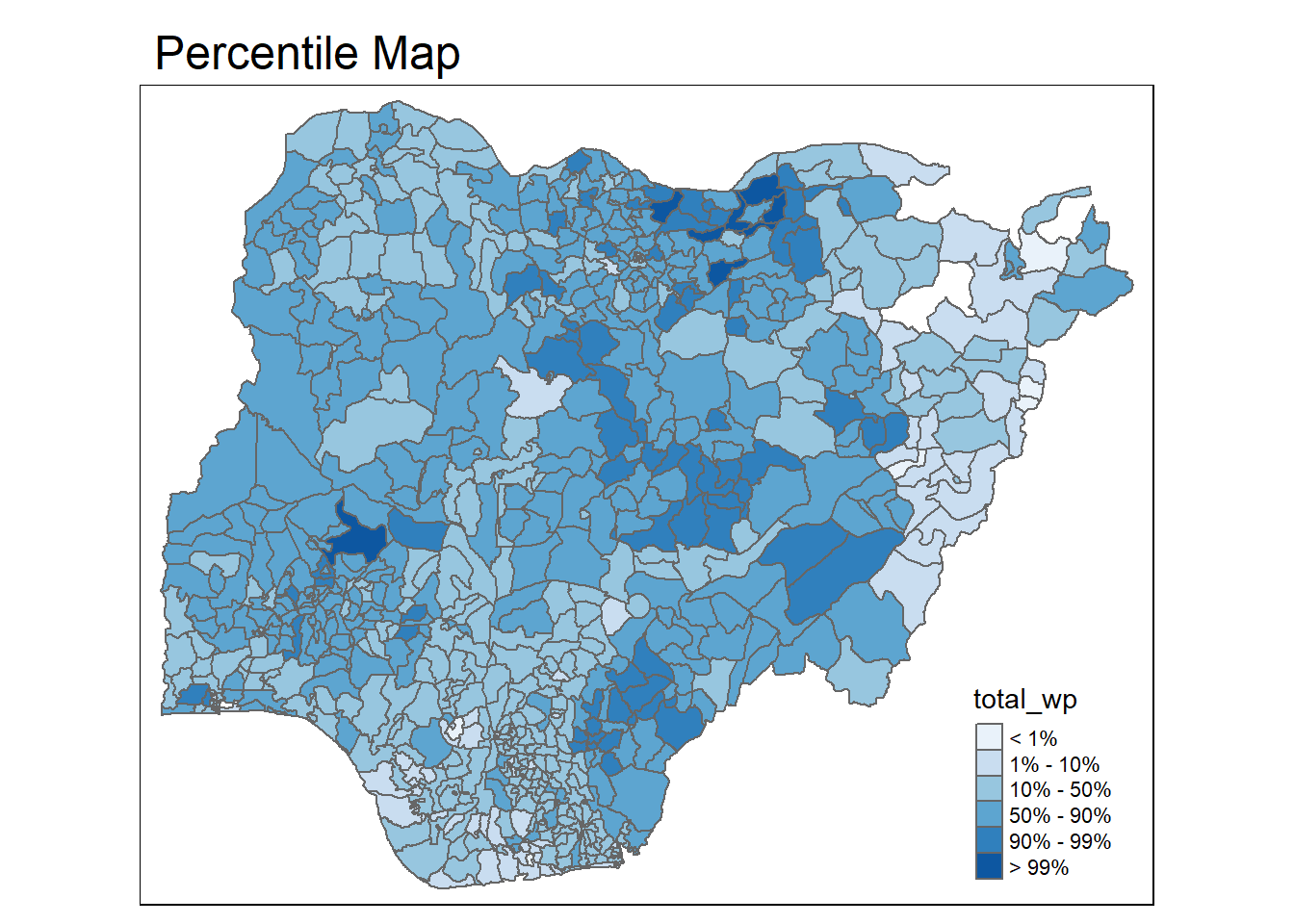
4.2 Box Map
Uses custom breaks specifications which depend on lower or upper outliers.
ggplot(data = NGA_wp,
aes(x = "",
y = wp_nonfunctional)) +
geom_boxplot()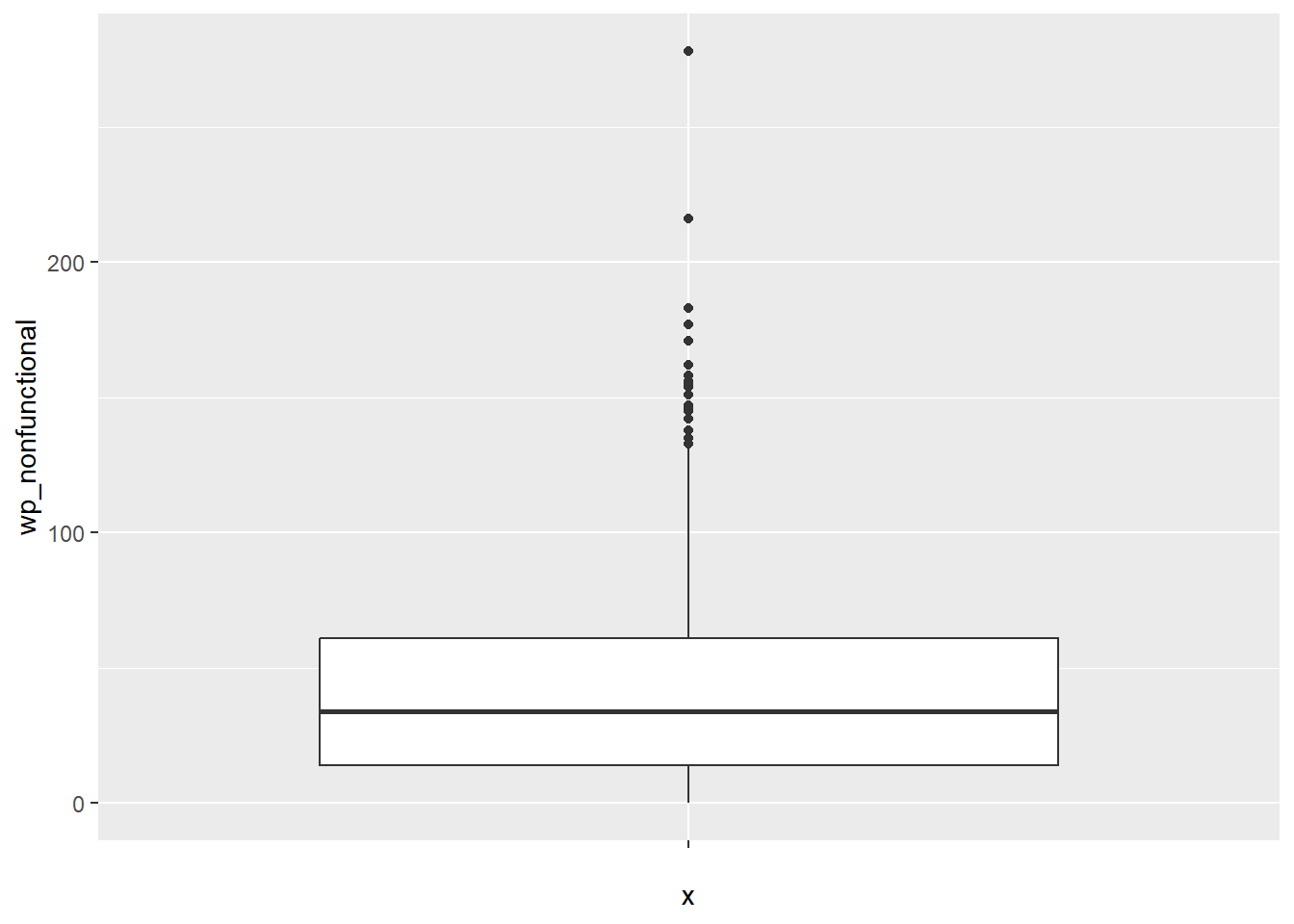
4.3 Boxbreak function
Similarly, functions can be created for custom boxbreaks
inputs:
v: vector with observations
mult: multiplier for IQR
output:
- bb: vector with 7 break points that compute quantile and fence
boxbreaks <- function(v,mult=1.5) {
qv <- unname(quantile(v))
iqr <- qv[4] - qv[2]
upfence <- qv[4] + mult * iqr
lofence <- qv[2] - mult * iqr
# initialize break points vector
bb <- vector(mode="numeric",length=7)
# logic for lower and upper fences
if (lofence < qv[1]) { # no lower outliers
bb[1] <- lofence
bb[2] <- floor(qv[1])
} else {
bb[2] <- lofence
bb[1] <- qv[1]
}
if (upfence > qv[5]) { # no upper outliers
bb[7] <- upfence
bb[6] <- ceiling(qv[5])
} else {
bb[6] <- upfence
bb[7] <- qv[5]
}
bb[3:5] <- qv[2:4]
return(bb)
}4.4 get.var function
inputs:
vname: variable name (as character in quotes)
df: name of the sf data frame
output:
- v: a vector with values (without column name)
get.var <- function(vname,df) { v <- df[vname] %>% st_set_geometry(NULL) v <- unname(v[,1]) return(v) }
4.5 Running the newly created function
var <- get.var("wp_nonfunctional", NGA_wp)
boxbreaks(var)[1] -56.5 0.0 14.0 34.0 61.0 131.5 278.04.6 Boxmap function
arguments:
vnam: variable name
df: simple feature polygon layer
legtitle: legend title
mtitle: map title
mult: multiplier for IQR
output: tmap element that plots the map
boxmap <- function(vnam, df,
legtitle=NA,
mtitle="Box Map",
mult=1.5){
var <- get.var(vnam,df)
bb <- boxbreaks(var)
tm_shape(df) +
tm_polygons() +
tm_shape(df) +
tm_fill(vnam,title=legtitle,
breaks=bb,
palette="Blues",
labels = c("lower outlier",
"< 25%",
"25% - 50%",
"50% - 75%",
"> 75%",
"upper outlier")) +
tm_borders() +
tm_layout(main.title = mtitle,
title.position = c("left",
"top"))
}tmap_mode("plot")
boxmap("wp_nonfunctional", NGA_wp)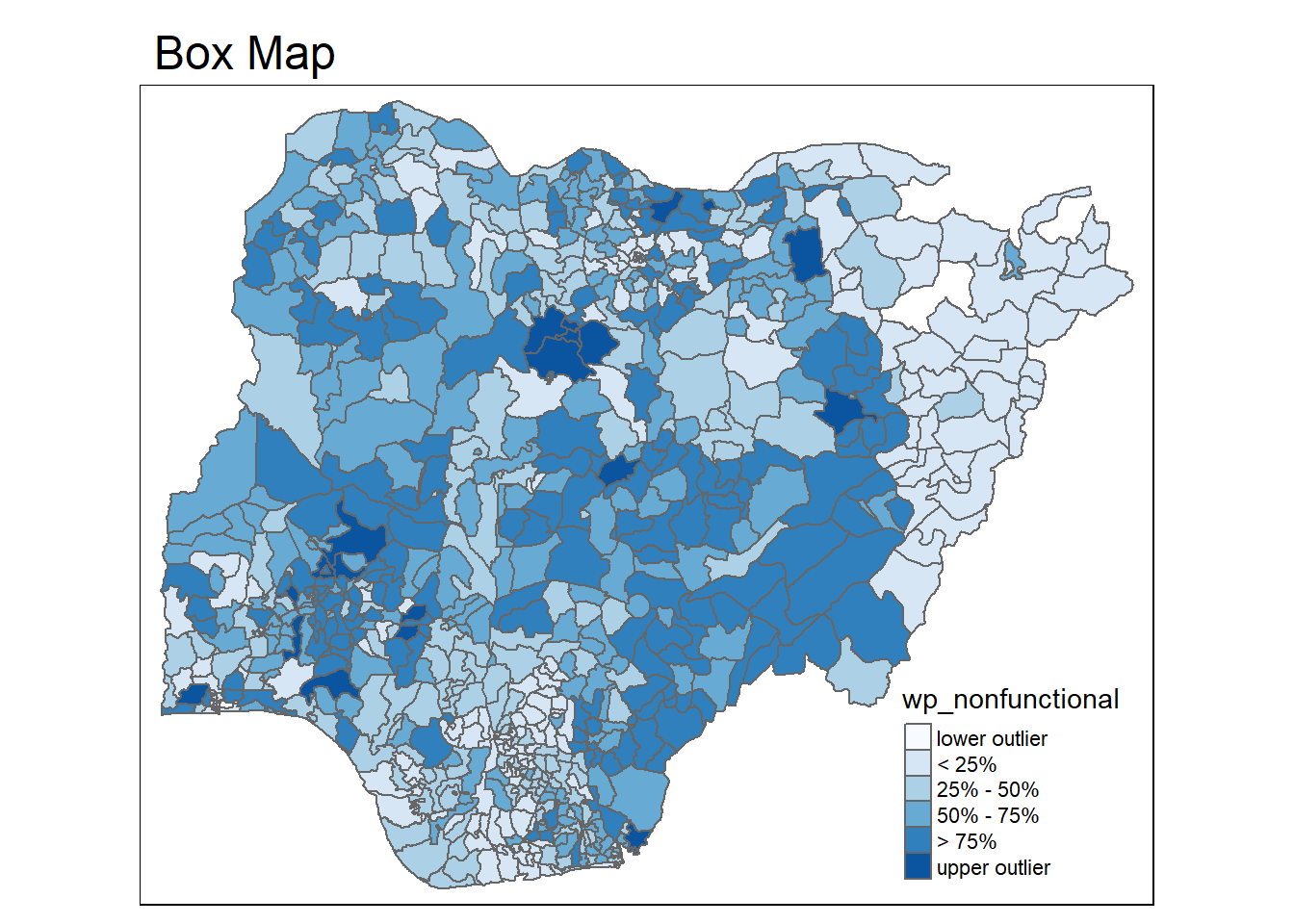
5 Recode
Recode LGAs with zero total water points to NA.
NGA_wp <- NGA_wp %>%
mutate(wp_functional = na_if(
total_wp, total_wp < 0))